Solution to puzzle 91: Nonagon diagonals
In regular nonagon ABCDEFGHI, show that AF = AB + AC.
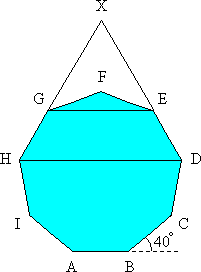
Continue DE and HG to meet at X.
By symmetry, AC = EG and AF = DH.
Also by symmetry, EG and DH are parallel to AB.
Line segment BC makes an angle of 360° / 9 = 40° with line segment AB (or its continuation.)
Hence CD makes an angle of 80° with AB, and DE makes an angle of 120° with AB.
Hence 
HDX = 60°. Similarly XHD = 60°, and so DXH = 60°.
It follows that 
XHD and XGE are both equilateral.
Hence DH = DX and EG = EX.
So, DX = DE + EX 
DH = DE + EG.
Therefore, in regular nonagon ABCDEFGHI, AF = AB + AC.
Alternative proof
Madhukar Daftary sent the following elegant solution.
Draw diagonals ID and IG. Let AF and ID intersect at O.
By symmetry, CD, AF, and IG are parallel. Similarly, AC and ID are parallel.
Also by symmetry,
AO = CD = AB
OF = IG = AC
Adding, we obtain
AF = AO + OF = AB + AC
Heptagon diagonals 
In regular heptagon ABCDEFG, show that 1/AB = 1/AC + 1/AE.
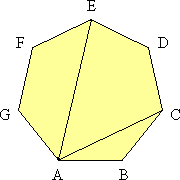
Hint - Solution
Further reading
Source: Original