Skip to main content.

Solution to puzzle 91 (Heptagon diagonals)

In regular heptagon ABCDEFG, show that 1/AB = 1/AC + 1/AE.

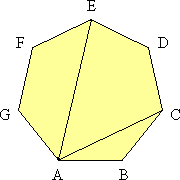
Regular heptagon ABCDEFG, showing diagonals AC and AE.

A regular heptagon is cyclic (as is as any regular polygon), and therefore any quadrilateral defined by four of its vertices is also cyclic.
Ptolemy's Theorem states that in a cyclic quadrilateral the sum of the products of the two pairs of opposite sides equals the product of its two diagonals.

Let AB = CD = DE = a, AC = CE = b, AD = AE = c.
Applying Ptolemy's Theorem to cyclic quadrilateral ACDE, we obtain ab + ac = bc.
Then a(b + c) = bc, and so 1/a = (b + c)/bc = 1/b + 1/c.

Therefore, in regular heptagon ABCDEFG, 1/AB = 1/AC + 1/AE.

Remarks

The nonagon diagonals puzzle may be solved by applying Ptolemy's Theorem to cyclic quadrilateral ABDG.

Further reading

  1. Ptolemy's Theorem and Interpolation
  2. Heptagon

Source: Mathematics: Problems of the Month (problem since taken down)

Back to top