Second hint to puzzle 152: Totient valence

A number of steps are needed to evaluate v(2¹⁰⁰⁰)...

Note that, if k = p₁^a₁ · p₂^a₂ ·...· p_r^a_r, then (k) = (p₁^a₁ − p₁^a₁−1)·(p₂^a₂ − p₂^a₂−1)·...·(p_r^a_r − p_r^a_r−1).  (1)

Show that:

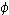• (2k) = 2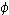(k), if k is even;
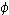• (2k) = 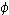(k), if k is odd.

Let k be such that (k) = 2^m, for some m.  Show that, if p is a prime that divides k, then p − 1 = (p) divides (k) = 2^m.  Hence the primes that make up k are of the form 2^t + 1.  (Note that if 2^t + 1 is prime then t is a power of 2.)  Then use (1) to find all odd k such that (k) = 2^m, for m < 32.