Solution to puzzle 126: Intersecting squares
The sides of two squares (not necessarily of the same size) intersect in eight distinct points: A, B, C, D, E, F, G, and H. These eight points form an octagon. Join opposite pairs of vertices to form two non-adjacent diagonals. (For example, diagonals AE and CG.) Show that these two diagonals are perpendicular.
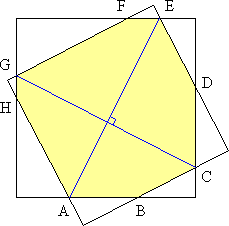
Denote by square 1 the square whose sides are parallel to AB and CD, and by square 2 the square whose sides are parallel to BC and DE. Rotate the whole figure one right angle counterclockwise about the center of square 1. Then superimpose this figure on the original figure, so that square 1 maps to itself, and square 2 maps to a rotated version of itself. Label the intersection points of square 1 and the rotated square 2: A', B', ... , H'. Draw C'G'. We will show that C'G' is parallel to AE.
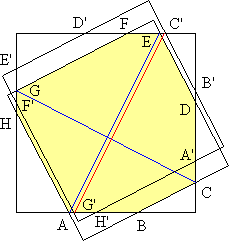
Square 2 maps to a translation of itself, so that B'C', DE, G'F', and AH are all parallel.
Hence C'E = G'A, and so AE is parallel to C'G'.
But C'G' is perpendicular to CG, as square 2 was rotated by a right angle, and therefore CG is perpendicular to AE.
Therefore, AE is perpendicular to CG; that is, two non-adjacent diagonals are perpendicular.
Source: Problem 2 in Mathematics Department Problem September, 2004 (document since taken down)