Skip to main content.

Solution to puzzle 115: Sum of sines

Skip restatement of puzzle.Let f(x) = sin(x) + sin(x°), with domain the real numbers.  Is f a periodic function?

(Note: sin(x) is the sine of a real number, x, (or, equivalently, the sine of x radians), while sin(x°) is the sine of x degrees.)

If f is periodic then so is its derivative, f '.  This follows by considering the definition of f '.  If f has period T, then, for any a:

f'(a) = limit as h tends to 0 of [f(a+h)-f(a)]/h = limit as h tends to 0 of [f(a+T+h)-f(a+T)]/h = f'(a+T)

We will show that f ' is not a periodic function and, hence, neither is f.

We have f(x) = sin(x) + sin(x°) = sin(x) + sin(pix/180).  (Since 360° = 2pi radians.)
Hence f '(x) = cos(x) + (pi/180) cos(pix/180).

Clearly, f '(0) = 1 + pi/180 is the maximum value of f ', attained only when both cosines are equal to 1.
Suppose f has period T.  Then f '(T) = f '(0).
But f '(T) = cos(T) + (pi/180) cos(Tpi/180).
Hence cos(T) = 1 and cos(Tpi/180) = 1.

cos(T) = 1 implies T = 2npi, for some integer n.
cos(Tpi/180) = 1 implies Tpi/180 = 2mpi, for some integer m.  Hence T = 360m.
Combining these two results, we conclude that pi = 180m/n.
We have reached a contradiction, as pi is known to be irrational.
Hence f ' is not a periodic function.

Therefore, f is not a periodic function.

Remarks

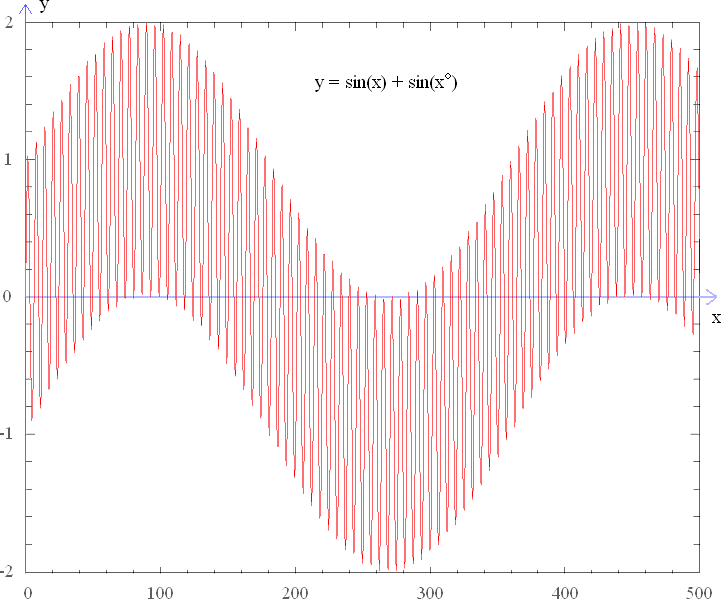
The graph of f for 0 less than or equal to x less than or equal to 500 is shown below.

Graph of y = f(x) for 0 <= x <= 500.

Further reading

  1. Periodic Function

Source: Original

Back to top