Solution to puzzle 103: Root sums
![]() Let a, b, c be rational numbers. Show that each of the following equations can be satisfied only if a = b = c = 0.
Let a, b, c be rational numbers. Show that each of the following equations can be satisfied only if a = b = c = 0.
- a + b
 + c
+ c = 0.
= 0. - a + b
 + c
+ c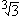 = 0.
= 0. - a + b
 + c
+ c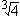 = 0.
= 0.
First of all, note that we may assume a, b, c are integers, for we can multiply each equation by the least common multiple of the denominators.
We will proceed by reductio ad absurdum; assume that each equation can be satisfied for non-zero a, b, c, and derive a contradiction. For this we will need the following lemma.
Lemma
Let n, m be positive integers, with n > 1. Then ![]() is either an integer or is irrational.
is either an integer or is irrational.
Proof
Suppose that ![]() = r/s is rational.
= r/s is rational.
Then rn = msn.
By the Fundamental Theorem of Arithmetic, both sides of the equation must have the same prime factorization.
In the prime factorizations of rn and sn, each prime occurs a multiple of n times.
Hence each prime in the prime factorization of m must occur a multiple of n times.
That is, m is an nth power, and ![]() is an integer.
is an integer.
We conclude that ![]() is either rational (in which case it's an integer), or is irrational.
is either rational (in which case it's an integer), or is irrational.
i. a + b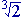 + c
+ c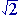 = 0
= 0
Firstly, we note that if b = c = 0, then a = 0.
If c = 0 and b ![]() 0, then
0, then ![]() = −a/b, contradicting the above lemma. (13 < 2 < 23
= −a/b, contradicting the above lemma. (13 < 2 < 23 ![]()
![]() is not an integer, and so must be irrational.)
is not an integer, and so must be irrational.)
If c ![]() 0, we rewrite the equation as −b
0, we rewrite the equation as −b![]() = a + c
= a + c![]() . Cubing both sides, we obtain
. Cubing both sides, we obtain
| −2b3 | = a3 + 3a2c |
| = a3 + 6ac2 + (3a2c + 2c3) |
Hence ![]() = −(2b3 + a3 + 6ac2)/(3a2c + 2c3). (Note that the denominator is necessarily non-zero.)
= −(2b3 + a3 + 6ac2)/(3a2c + 2c3). (Note that the denominator is necessarily non-zero.)
Again, this contradicts the lemma.
Therefore the only solution is a = b = c = 0.
ii. a + b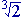 + c
+ c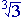 = 0
= 0
Note that if a = 0, then b = c = 0, for otherwise ![]() is rational, and so 2 ×
is rational, and so 2 × ![]() =
= ![]() is rational, contradicting the above lemma.
is rational, contradicting the above lemma.
If b = 0, then a = c = 0, for otherwise ![]() = −a/c is rational.
= −a/c is rational.
If c = 0, then a = b = 0, for otherwise ![]() = −a/b is rational.
= −a/b is rational.
Now suppose a, b, c are non-zero, and rewrite the equation as −a = b![]() + c
+ c![]() . Making use of the identity (x + y)3 = x3 + y3 + 3xy(x + y), and cubing both sides, we obtain
. Making use of the identity (x + y)3 = x3 + y3 + 3xy(x + y), and cubing both sides, we obtain
| −a3 | = 2b3 + 3c3 + 3bc |
| = 2b3 + 3c3 − 3abc |
Now ![]() = (a3 + 2b3 + 3c3)/3abc, contradicting the lemma.
= (a3 + 2b3 + 3c3)/3abc, contradicting the lemma.
Therefore the only solution is a = b = c = 0.
iii. a + b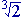 + c
+ c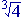 = 0
= 0
As above, we can conclude that if one of a, b, c equals zero, then all must equal zero. We now assume a, b, c are all non-zero.
Rewrite the equation as −a = b![]() + c
+ c![]() . Making use of the identity (x + y)3 = x3 + y3 + 3xy(x + y), and cubing both sides, we obtain
. Making use of the identity (x + y)3 = x3 + y3 + 3xy(x + y), and cubing both sides, we obtain
| −a3 | = 2b3 + 4c3 + 6bc(b |
| = 2b3 + 4c3 − 6abc |
Hence a3 + 2b3 + 4c3 − 6abc = 0.(1)
We now assume that the greatest common divisor of a, b, c is 1. (If not, we can divide a, b, c by their greatest common divisor.)
From (1), a is even. Let a = 2a1.
Then 8a13 + 2b3 + 4c3 − 12a1bc = 0, from which 4a13 + b3 + 2c3 − 6a1bc = 0.
Hence b is even. Let b = 2b1.
Then 4a13 + 8b13 + 2c3 − 12a1b1c = 0, from which 2a13 + 4b13 + c3 − 6a1b1c = 0.
We now conclude that c is even, so that a, b, c are all even. This is a contradiction, as we assumed that the greatest common divisor of a, b, c is 1.
Therefore the only solution is a = b = c = 0.
Sum of two squares 
Show that a2 + b2 = 3c2 has no solution in positive integers.
Hint - Solution
Quadratic roots 
Find a necessary and sufficient condition for one of the roots of x2 + ax + b = 0 to be the square of the other root.
Hint - Answer - Solution
Further reading
- Infinite Descent
- Irrationality by Infinite Descent
- Fermat's Infinite Descent
- Infinite Descent versus Induction
Source: Traditional