Skip to main content.

Solution to puzzle 73: Unobtuse triangle

Skip restatement of puzzle.A triangle has internal angles A, B, and C, none of which exceeds 90°.  Show that

sin A + sin B + sin C > 2

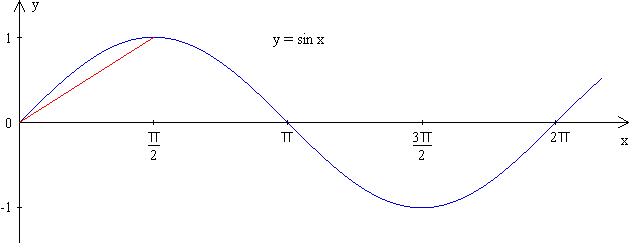
Consider the graph of y = sin x, below, and the line segment joining the origin to the point (pi/2,1).
Note that the second derivative, y'' = −sin x, is negative for 0 < x < pi/2, and so that section of the graph is concave.
The equation of the line segment is y = (2/pi) · x.  Note that the line segment intersects the concave curve at x = 0 and x = pi/2.
Hence, for 0 < x less than or equal to pi/2, we have sin x greater than or equal to (2/pi) · x, with equality only for x = pi/2.
Since 0 < A, B, C less than or equal to pi/2, with equality in at most one case, we have: sin A + sin B + sin C > (2/pi) · (A + B + C).
Since A + B + C = pi, it follows that sin A + sin B + sin C > 2.

Graph of y = sin x. Superimposed is the line segment joining the origin to the point (pi/2,1).

By judicious choice of line segment we can similarly establish the other two results.

cos A + cos B + cos C > 1

Consider the graph of y = cos x, below, and the line segment from (0,1) to (pi/2,0).
The second derivative, y'' = −cos x, is negative for 0 < x < pi/2, and so that section of the graph is concave.
The equation of the line segment is y = 1 − (2/pi) · x.
Hence, for 0 < x less than or equal to pi/2, we have cos x greater than or equal to 1 − (2/pi) · x, with equality only for x = pi/2.
Then cos A + cos B + cos C > 3 − (2/pi) · (A + B + C).
Therefore cos A + cos B + cos C > 1.

Graph of y = cos x. Superimposed is the line segment joining the points (0,1) and (pi/2,0).

tan (A/2) + tan (B/2) + tan (C/2) < 2

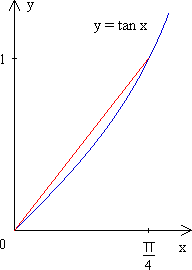
Finally, consider the graph of y = tan x, and the line segment from the origin to (pi/4,1).
The second derivative, y'' = 2 tan x sec2 x, is positive for 0 < x < pi/4, and so that section of the graph is convex.
The equation of the line segment is y = (4/pi) · x.
Hence, for 0 < x less than or equal to pi/4, we have tan x less than or equal to (4/pi) · x, with equality only for x = pi/4.
Then tan (A/2) + tan (B/2) + tan (C/2) < (4/pi) · (A/2 + B/2 + C/2).
Therefore tan (A/2) + tan (B/2) + tan (C/2) < 2.

Graph of y = tan x. Superimposed is the line segment joining the origin to the point (pi/4,1).

Remarks

A real-valued function is said to be convex on an interval I if, and only if

f(ta + (1 − t)b) less than or equal to tf(a) + (1 − t)f(b)

for all a, b in I and 0 less than or equal to t less than or equal to 1.  It can be shown that if f''(x) greater than or equal to 0 for all x in I, then f is convex on I.  A real-valued function is said to be concave on an interval I if, and only if, −f is convex on I.

Further reading

  1. Jensen's Inequality
  2. (Adobe) Portable Document Format Inequalities and Triangles
  3. Triangle Inequalities

Source: Original

Back to top