Solution to puzzle 69: Combinatorial sum

The result will be obtained in two steps.

1. Show that, for any positive integer, r
   
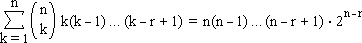
2. Express k⁵ in terms of  k,  k(k − 1),  k(k − 1)(k − 2),  k(k − 1)(k − 2)(k − 3), and  k(k − 1)(k − 2)(k − 3)(k − 4).

Step 1

This result may be proved by means of a direct counting, or combinatorial, argument.

The number of ways of choosing, from n people, a committee of k > 0 members; and, from the committee, a set of r > 0 distinct officials (chairperson, vice-chairperson, secretary...) is

Summing over all values of k, that is, from 1 to n, we have the left-hand side of equation 1, above.  This is the total number of ways of choosing a committee, with r distinct officials.

Counting the same objects in a different way, we can choose the chairperson, vice-chairperson, secretary... in n(n − 1) ... (n − r + 1) ways, and the remaining members of the committee in 2^n−r ways.
Hence the number of ways of choosing a committee, with r distinct officials, is n(n − 1) ... (n − r + 1) · 2^n−r, which is the right-hand side of equation 1.
The result follows.

Step 2

In order to make use of the above result, we must express k⁵ in terms of  k,  k(k − 1),  k(k − 1)(k − 2),  k(k − 1)(k − 2)(k − 3), and  k(k − 1)(k − 2)(k − 3)(k − 4).
We can do this by using Newton's forward difference formula.  (See also Finite difference.)

Firstly, we draw up the difference table for k⁵, beginning at k = 0.

0		1		32		243		1024		3125		7776
	1		31		211		781		2101		4651
		30		180		570		1320		2550
			150		390		750		1230
				240		360		480
					120		120
						0

Reading off the first number in each row, and, for the rth difference row, dividing by r!, we have

k⁵  =  k  +  15k(k − 1)  +  25k(k − 1)(k − 2)  +  10k(k − 1)(k − 2)(k − 3)  +  k(k − 1)(k − 2)(k − 3)(k − 4).

Putting the steps together

	=  n · 2n−1  +  15n(n − 1) · 2n−2  +  25n(n − 1)(n − 2) · 2n−3  +  10n(n − 1)(n − 2)(n − 3) · 2n−4  +  n(n − 1)(n − 2)(n − 3)(n − 4) · 2n−5
	=  2n−5 [16n  +  120n(n − 1)  +  100n(n − 1)(n − 2)  +  20n(n − 1)(n − 2)(n − 3)  +  n(n − 1)(n − 2)(n − 3)(n − 4)]
	=  n2(n3 + 10n2 + 15n − 10) · 2n−5

---

Remarks

Equation 1, above, can also be derived from the binomial theorem.

Differentiating, with respect to x, both sides of

we get

and, with x = 1, we have

This is equation 1, for r = 1.  A further differentiation would yield equation 1, for r = 2, and so on.

---

Further reading

1. Umbral calculus
2. Binomial sums

Source: Traditional

Back to top