Skip to main content.

Solution to puzzle 59: Triangle inequality

A triangle has sides of length a, b, and c.  Show that   3/2 <= a/(b+c) + b/(c+a) + c/(a+b) < 2.

Left inequality

The left side of the inequality is, in fact, true for all triples (a, b, c) of positive real numbers.  We can prove it using the rearrangement inequality, stated below.

Let a1 less than or equal to a2 less than or equal to ... less than or equal to an and b1 less than or equal to b2 less than or equal to ... less than or equal to bn be real numbers.  For any permutation (c1, c2, ..., cn) of (b1, b2, ..., bn), we have:

a1b1 + a2b2 + ... + anbn  greater than or equal to  a1c1 + a2c2 + ... + ancn  greater than or equal to  a1bn + a2bn−1 + ... + anb1,

with equality if, and only if, (c1, c2, ..., cn) is equal to (b1, b2, ..., bn) or (bn, bn−1, ..., b1), respectively.

That is, the sum is maximal when the two sequences, {ai} and {bi}, are sorted in the same way, and is minimal when they are sorted oppositely.

Now we apply the rearrangement inequality to suitably chosen sequences.  Specifically, we will use the result that the sum is maximal when the two sequences are sorted in the same way.

Without loss of generality, assume a less than or equal to b less than or equal to c.
Then the sequences {a, b, c} and  {1/(b+c), 1/(c+a), 1/(a+b)}  are sorted the same way.

We twice rotate the second sequence, and apply the rearrangement inequality, to obtain:

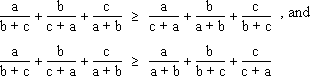
a/(b+c) + b/(c+a) + c/(a+b) >= a/(c+a) + b/(a+b) + c/(b+c), and a/(b+c) + b/(c+a) + c/(a+b) >= a/(a+b) + b/(b+c) + c/(c+a).

Adding these two inequalities, and dividing by two, we get   a/(b+c) + b/(c+a) + c/(a+b) >= 3/2.

We must also show that equality can occur, which is readily seen by setting a = b = c.

Right inequality

In order to prove the right inequality, we must use the fact that a, b, c are the sides of a triangle.

Let s = ½(a + b + c) be the semi-perimeter of the triangle.
In any triangle, a + b > c, and so a + b > s.

Hence   c/(a+b) < c/s,  and similarly   a/(b+c) < a/s, b/(c+a) < b/s.

Adding the three inequalities, we get   a/(b+c) + b/(c+a) + c/(a+b) < (a+b+c)/s.

Therefore   a/(b+c) + b/(c+a) + c/(a+b) < 2.

Additional puzzle

The following inequality is due to Gheorge Eckstein.

Let a, b, x, y, z be positive real numbers.  Show that:

x/(ay+bz) + y/(az+bx) + z/(ax+by) >= 3/(a+b).

Further reading

  1. (Adobe) Portable Document Format The Rearrangement Inequality by K. Wu and Andy Liu -- a tutorial that shows how to derive many other inequalities, such as Arithmetic Mean - Geometric Mean, Geometric Mean - Harmonic Mean, and Cauchy-Schwartz, from the Rearrangement Inequality.
  2. The left inequality is known as Nesbitt's Inequality.
  3. Shapiro's Cyclic Sum Constant

Source: Traditional

Back to top